1. Kaj je ulomek
Ulomek je število, ki določa delež celote, razdeljene na enake dele. Zapišemo ga v obliki dveh števil, ki sta med seboj ločeni z vodoravno črto. Zgornje število imenujemo števec, spodnje število pa imenovalec.
Imenovalec nam pove, na koliko enakih delov je razdeljena celota, števec pa, koliko takšnih delov predstavlja naš delež.
Primer ulomka je 3⁄4, kjer 3 predstavlja število delov celote (števec), 4 pa število enakih delov, na katere je celota razdeljena (imenovalec).
Kako ponazorimo ulomek
Ulomek je del celote, zato si ga najlažje predstavljamo z opazovanjem konkretnih celot in njihovih delov. Pri tem si najpogosteje pomagamo z geometrijskimi liki, kot so krogi ali pravokotniki. Na primer, če želimo prikazati ulomek 3⁄4:
1. Lik razdelimo na štiri enake dele (imenovalec).
2. Tri dele pobarvamo (števec).
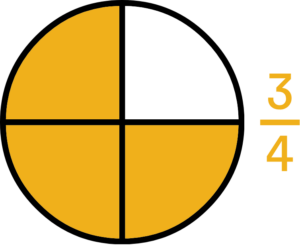
S to grafično ponazoritvijo lažje razumemo, kaj ulomek predstavlja in kako deluje.
Prikaz ulomka na številski premici
Ulomke lahko prikažemo tudi na številski premici. Tako vidimo, kako veliki so in kako daleč so od izhodišča. V postopku umeščanja ulomka na številsko os:
- Upoštevamo celi del ulomka in se premaknemo za toliko števil v desno.
- Desno od tega števila upoštevamo še ulomkov neceli del, tako da ga prikažemo kot del celote do naslednjega naravnega števila.
Na primer, ulomek 3⁄4 bi na številski premici umestili med 0 in 1, bližje številu 1.
2. Vrste ulomkov
Pravi ulomki
Pravi ulomek je ulomek, kjer je števec manjši od imenovalca. To pomeni, da je vrednost ulomka manjša od 1.
Na primer, ulomek 2⁄3 je pravi ulomek, saj je 2 manjše od 3.
Nepravi ulomki
Nepravi ulomek je ulomek, kjer je števec večji ali enak imenovalcu. To pomeni, da je vrednost ulomka večja ali enaka 1.
Na primer, ulomek 5⁄4 je nepravi ulomek, saj je 5 večje od 4.
Takšen ulomek lahko zapišemo tudi kot mešano število, torej kot kombinacijo celega števila in pravega ulomka: 1 1⁄4.
Mešana števila
Mešano število je sestavljeno iz celega dela in ulomka.
Na primer, 2 1⁄3 je mešano število, kjer 2 predstavlja celote, 1⁄3 pa dodatni del celote.
Mešana števila so koristna, če želimo predstaviti neprave ulomke v bolj jasni (in razumljivi) obliki.
Ulomki, ki jih lahko zapišemo kot naravna števila
Če je števec ulomka večkratnik imenovalca, se deljenje izide in ulomek lahko zapišemo kot naravno število.
Na primer, 4⁄2 je enako 2.
Enako velja obratno: vsako naravno število lahko zapišemo kot ulomek, tako da pod številko dopišemo ulomkovo črto in v imenovalec zapišemo 1.
Na primer, naravno število 3 lahko zapišemo kot ulomek 3⁄1.
S temi osnovami o vrstah ulomkov boste lažje razumeli in izvajali operacije z ulomki, kot so seštevanje, odštevanje, množenje in deljenje ulomkov.
3. Računanje z ulomki
Računanje z ulomki je lahko preprosto, če se ga lotite pravilno. V tem poglavju vas bomo vodili skozi ključne korake, kot so razširjanje, krajšanje ter primerjava in urejanje ulomkov po velikosti. S temi osnovnimi veščinami boste kos vsem izzivom, ki jih lahko ponudi matematika.
Razširjanje ulomkov
Razširjanje ulomkov pomeni, da števec in imenovalec pomnožite z enakim številom, ki ni 0 ali 1. To je zelo koristno, kadar morate seštevati ali odštevati ulomke z različnimi imenovalci.
Razširjanje ulomka primer:
Predstavljajte si ulomek 2⁄3. Razširimo ga s številom 4:
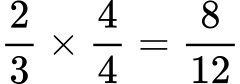
Tako smo ulomek zapisali v drugačni obliki, vendar njegova vrednost ostaja nespremenjena.
Krajšanje ulomkov
Krajšanje ulomkov pomeni, da števec in imenovalec delite z največjim skupnim deliteljem (NSD). S tem ulomek poenostavite (ga okrajšate) in ga naredite bolj preglednega.
Krajšanje ulomka primer:
Poglejmo ulomek 8⁄12 in ga okrajšajmo. Njegov največji skupni delitelj (NSD) je 4:
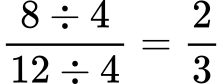
Zdaj imate poenostavljeno obliko ulomka, ki pa še vedno predstavlja enako vrednost.
Primerjava in urejanje ulomkov po velikosti
Primerjava in urejanje ulomkov po velikosti je pomembna veščina, s pomočjo katere lahko razumete relativne vrednosti ulomkov.
Ulomki z enakimi imenovalci:
Kadar imajo ulomki enake imenovalce, je enostavno. Primerjate števce in tisti ulomek, ki ima večji števec, je večji.
Primer:
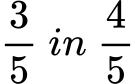
4⁄5 je večji, ker je 4 večje od 3.
Ulomki z enakimi števci:
Kadar imajo ulomki enake števce, je večji tisti, ki ima manjši imenovalec.
Primer:
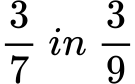
Ulomek 3⁄7 je večji, ker je 7 manjše od 9.
Ulomki z različnimi števci in imenovalci:
Kadar imajo ulomki različne števce in imenovalce, jih morate najprej razširiti na skupni imenovalec, preden jih primerjate.
Primer:

Razširimo ulomke na skupni imenovalec 12:
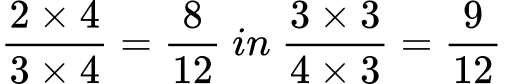
Zdaj je jasno, da je 9⁄12 večji od 8⁄12.
4. Osnovne operacije z ulomki
Ulomki omogočajo izvajanje osnovnih aritmetičnih operacij, kot so seštevanje, odštevanje, množenje in deljenje ulomkov. V tem poglavju bomo razložili, kakšna so pravila za računanje ulomkov.
Seštevanje ulomkov
Seštevanje ulomkov je preprosto, če imajo ulomki enake imenovalce. V tem primeru preprosto seštejete števce, imenovalec pa ostane enak.
Seštevanje ulomkov primer:

Če imajo ulomki različne imenovalce, jih morate najprej razširiti na skupni imenovalec.
Seštevanje ulomkov primer 2:
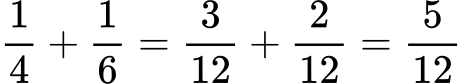
Odštevanje ulomkov
Odštevanje ulomkov deluje na enak način kot seštevanje. Če imajo ulomki enake imenovalce, odštejete števce, imenovalec ostane enak.
Odštevanje ulomkov primer:
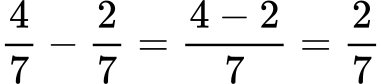
Pri različnih imenovalcih jih najprej razširite na skupni imenovalec.
Odštevanje ulomkov primer 2:
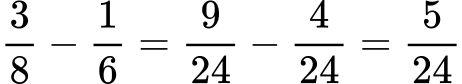
Množenje ulomkov
Množenje ulomkov je precej preprosto. Med seboj pomnožite števca in imenovalca.
Množenje ulomkov primer:
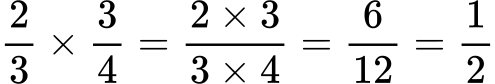
Deljenje ulomkov
Deljenje ulomkov je le nekoliko bolj zapleteno. Namesto deljenja deljenec pomnožite z obratno vrednostjo delitelja.
Deljenje ulomkov primer:

Deljenje ulomkov vaje
Za utrjevanje znanja o deljenju ulomkov, rešite naslednje vaje z rešitvami:
Deljenje ulomkov vaja 1:

Rešitev:
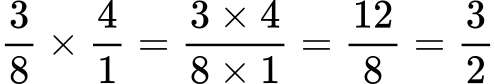
Deljenje ulomkov vaja 2:

Rešitev:
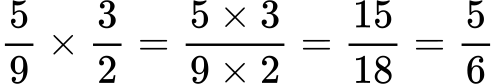
Z vajami in primeri boste z lahkoto obvladali deljenje ulomkov.
5. Decimalna števila
Decimalna števila in ulomki so nepogrešljiv del matematike. Kako pretvoriti decimalno število v ulomek in ulomek v decimalno število je nepogrešljiva operacija, ki jo morate obvladate, če želite uspešno reševati matematične probleme. Ogledali si bomo tudi zaokroževanje decimalnih števil.
Decimalna števila so številke, ki za prikaz delov celote vsebujejo decimalno vejico. Uporabljamo jih za bolj natančen prikaz vrednosti, ki niso cela števila.
Decimalna števila primer:
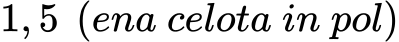
Decimalna števila so zelo uporabna pri merjenju, denarnih transakcijah in mnogih drugih praktičnih situacijah.
Ulomek v decimalno število
Ulomek pretvorite v decimalno število tako, da števec delite z imenovalcem. Ta postopek vam omogoča, da ulomek izrazite v obliki decimalnega števila, kar je pri vsakdanjih izračunih pogosto bolj uporabno.
Kako pretvorimo ulomek v decimalno število primer:
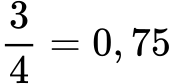
To dosežete tako, da 3 delite s 4, rezultat pa je 0,75.
Decimalno število v ulomek
Pretvorba decimalnega števila v ulomek zahteva nekoliko več dela, vendar je postopek precej preprost. Decimalno število zapišete kot ulomek z imenovalcem, ki je potenca števila 10, nato pa ulomek okrajšate, če je mogoče.
Kako pretvorimo decimalno število v ulomek primer:
Pretvorimo 0,6 v ulomek.
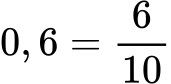
Nato ulomek okrajšamo z deljenjem števca in imenovalca z največjim skupnim deliteljem (v tem primeru je to 2):
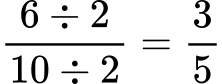
Zaokroževanje decimalnih števil
Zaokroževanje decimalnih števil je proces prilagajanja decimalnega števila na bližjo zaželeno vrednost. To je še posebej koristno, ko potrebujete približno vrednost ali ko delate z omejenim številom decimalk.
Kako zaokrožujemo decimalna števila?
- Pogledate števko na želenem decimalnem mestu.
- Če je števka na naslednjem mestu 5 ali več, povečate želeno števko za 1.
- Če je števka na naslednjem mestu manj kot 5, želeno števko pustite nespremenjeno.
Zaokroževanje decimalnih števil primer:
Zaokrožite decimalno število 3,146 na dve decimalni mesti.
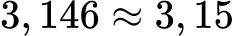
Ker je števka na tretjem decimalnem mestu 6, povečamo drugo decimalno mesto za 1.
Zaokroževanje je koristno pri reševanju problemov, kjer natančnost do več decimalnih mest ni potrebna.
6. Napredne operacije z ulomki
Napredne operacije z ulomki vam omogočajo reševanje kompleksnejših matematičnih problemov. V tem poglavju bomo obravnavali enačbe z ulomki, uporabo decimalnih števil in množenje decimalnih števil.
Enačbe z ulomki
Enačbe z ulomki so enačbe, ki vsebujejo enega ali več ulomkov. Reševanje teh enačb zahteva precejšnjo natančnost in pozornost. Več o reševanju enačb z ulomki tukaj.
Primer:
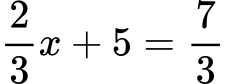
Kako rešujemo enačbe z ulomki?
- Znebite se ulomkov tako, da pomnožite obe strani enačbe z najmanjšim skupnim večkratnikom (NSV) imenovalcev.
- Rešite linearno enačbo.
- Preverite rešitev.
Množenje decimalnih števil
Množenje decimalnih števil je podobno množenju celih števil, vendar morate biti pozorni na decimalna mesta.
Koraki za množenje decimalnih števil:
- Množenje: Ignorirajte decimalne vejice in pomnožite števili kot celi števili.
- Decimalna mesta: Seštejte število decimalnih mest v obeh številih. V produktu dodajte enako število decimalnih mest.
- Zapišite rezultat: Zapišite produkt z ustreznimi decimalnimi mesti.
Množenje decimalnih števil primer:

1. Množenje brez decimalnih mest:

2. Seštejte decimalna mesta:
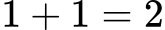
3. Dodajte decimalna mesta v produktu:

Množenje decimalnih števil je uporabno, ko računate površino, volumen in druge kvantitativne vrednosti v vsakodnevnih situacijah.
Decimalna števila in ulomki vaje z rešitvami
Spodaj smo pripravili matematične naloge: decimalna števila in ulomki. Rešite jih in utrdite, kaj je ulomek, množenje ulomkov, seštevanje ulomkov, zaokroževanje decimalnih števil in decimalno število v ulomek. Rešitve za računanje ulomkov najdete čisto spodaj. ⬇️
1. Odštevanje in seštevanje ulomkov – izračunajte vsoto in razliko ulomkov, rezultat okrajšajte:
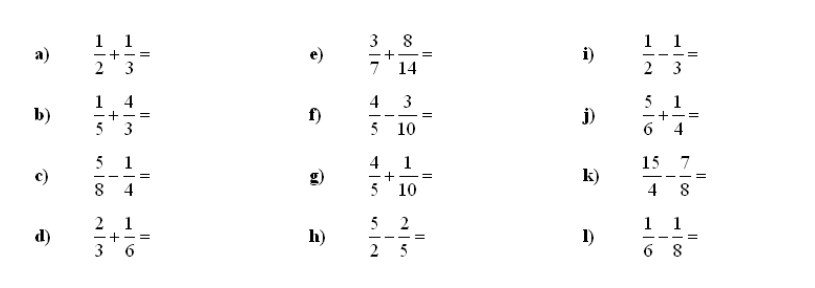
2. Množenje in deljenje ulomkov – izračunajte zmnožek in količnik ulomka, rezultat okrajšajte:
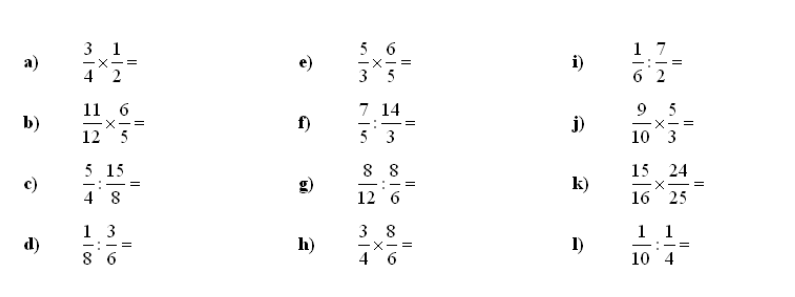
3. Mešano število pretvori v ulomek:
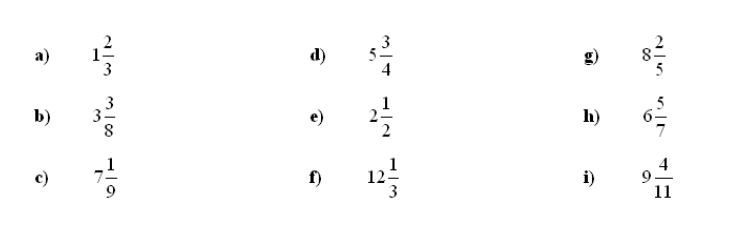
4. Ulomek pretvori v mešano število:
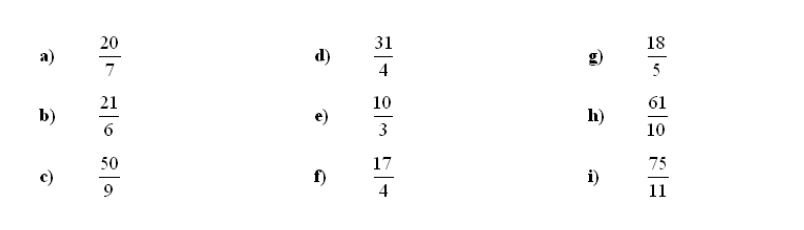
5. Pretvori decimalno število v ulomek in rezultat okrajšajte:

6. Računanje z ulomki – izračunajte in uredite rezultat:
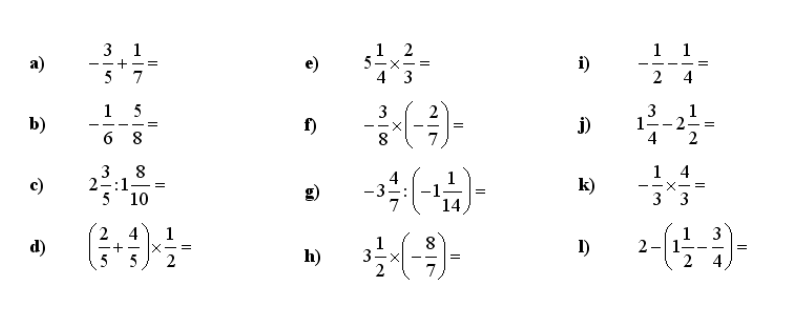
7. Računanje z ulomki – izračunajte in rezultat okrajšajte:
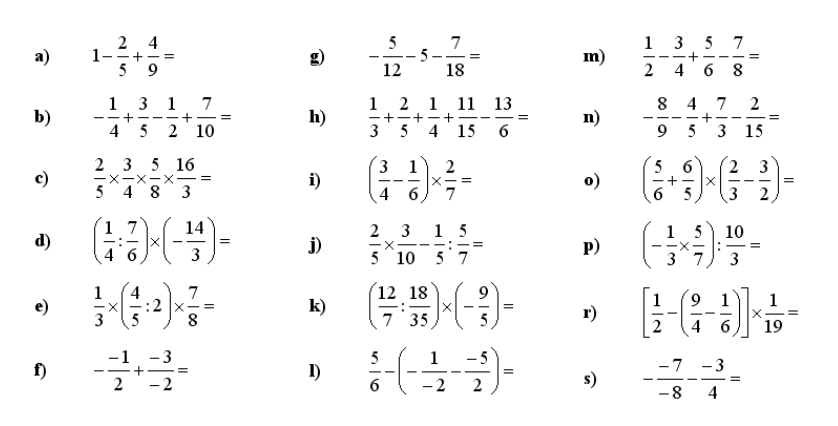
8. Računanje dvojnih ulomkov – razreši dvojni ulomek:
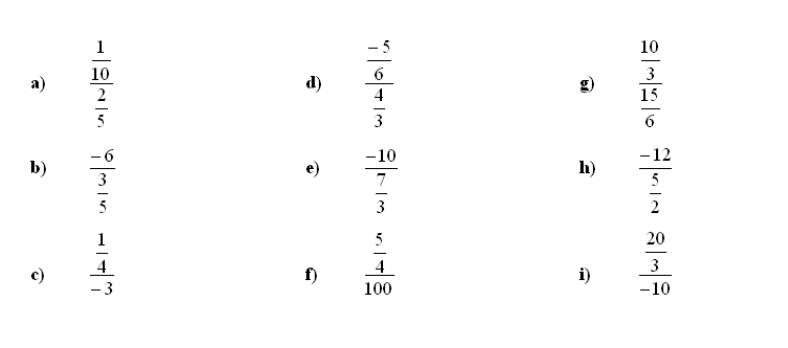

Vabljeni k reševanju drugih nalog – matematične vaje z rešitvami
Če iščete učitelja, ki vam lahko pomaga osvojiti decimalna števila in računanje z ulomki, hitro poiščite “inštruktor matematike Ljubljana” ali “inštrukcije matematike Celje”. Na platformah, kot je meet’n’learn, se lahko v trenutku povežete z najboljšim zasebnim učiteljem.
