Obseg in ploščina likov
Obseg in ploščina likov sta osnovni količini pri delu z geometrijskimi liki. Obseg opiše dolžino roba lika, ploščina pa pove, koliko enotskih kvadratkov prekrije dani lik. Uporabljajmo merske enote centimetre ali metre za dolžino, kvadratne centimetre ali kvadratne metre za ploščino.
🟠 Kaj pomeni obseg likov
Obseg je vsota vseh dolžin, ki omejujejo geometrijski lik. Označimo ga s črko $o$. Merimo ga v centimetrih ($\text{cm}$), metrih ($\text{m}$) ali drugih enotah za dolžino.
Izračunajmo obseg za nekaj osnovnih likov:
- Trikotnik s stranicami $a$, $b$ in $c$:
$o = a + b + c$ - Pravokotnik s stranicama $a$ in $b$:
$o = 2a + 2b$ - Kvadrat s stranico $a$:
$o = 4a$ - Krog s polmerom $r$:
$o = 2\pi r$
Če ima lik ukrivljene robove, obseg izračunamo s formulo za dolžino krivulje, na primer za krog s polmerom $r$ uporabimo $2\pi r$.
Obseg in ploščina pri osnovnih likih
Obseg in ploščina likov sta osnovni količini pri delu z ravninskimi geometrijskimi liki. Z obsegom izmerimo dolžino roba lika, s ploščino pa površino, ki jo lik pokriva. Pri tem uporabljajmo enote centimetre ($\text{cm}$), metre ($\text{m}$), kvadratne centimetre ($\text{cm}^2$) ali kvadratne metre ($\text{m}^2$).
🟠 Obseg likov kot vsota robov
Obseg geometrijskega lika izračunamo kot vsoto dolžin vseh njegovih robov. Označimo ga s črko $o$.
Za osnovne like uporabimo naslednje formule:
Trikotnik s stranicami $a$, $b$ in $c$: $o = a + b + c$
Pravokotnik s stranicama $a$ in $b$: $o = 2a + 2b$
Kvadrat s stranico $a$: $o = 4a$
Krog s polmerom $r$: $o = 2\pi r$
Pri likih z ukrivljenimi robovi, kot je krog, dolžino roba (obseg) določimo s pomočjo formule za dolžino krožnice. Uporabimo $2\pi r$, kjer je $r$ polmer.
🟠 Ploščina likov kot štetje kvadratkov
Ploščina pove, koliko enotskih kvadratkov bi potrebovali, da povsem prekrijemo notranjost lika. Označimo jo s črko $p$ ali $S$, najpogosteje pa uporabimo $p$.
Ploščino izražamo v kvadratnih enotah, kot so $\text{cm}^2$ ali $\text{m}^2$.
Za osnovne like uporabimo naslednje formule:
Pravokotnik s stranicama $a$ in $b$: $p = a \cdot b$
Kvadrat s stranico $a$: $p = a^2$
Trikotnik s stranico $a$ in višino $v$ na to stranico: $p = \frac{1}{2}av$
Krog s polmerom $r$: $p = \pi r^2$
Ploščina je vedno pozitivno število in odraža dejansko velikost pokrite ravninske površine. Pri sestavljenih likih razdelimo lik na enostavne dele, za katere lahko uporabimo znane formule, ter ploščine teh delov seštejemo.
Ploščina kvadrata in obseg kvadrata
Kvadrat je štirikotnik, pri katerem so vse stranice enako dolge, vsi koti pa merijo $90^\circ$. Ker so vse stranice enake, so računi za obseg in ploščino preprosti.
🟠 Formula za obseg kvadrata
Obseg kvadrata izračunamo tako, da dolžino stranice pomnožimo s štiri:
$o = 4a$
Če je stranica dolga $7,\text{cm}$, potem:
$o = 4 \cdot 7$
$o = 28,\text{cm}$
🟠 Formula za ploščino kvadrata
Ploščino kvadrata dobimo tako, da dolžino stranice kvadriramo:
$p = a^2$
Rezultat vedno izrazimo v kvadratnih enotah, na primer v kvadratnih centimetrih ($\text{cm}^2$) ali kvadratnih metrih ($\text{m}^2$).
Če je stranica dolga $5,\text{cm}$, izračunamo:
$p = 5^2$
$p = 25,\text{cm}^2$
Ploščina kroga in obseg kroga
Krog je ravninski lik, ki ga omejuje krožnica. Vse točke na krožnici so od središča enako oddaljene. To razdaljo imenujemo polmer ($r$). S polmerom izračunamo obseg in ploščino kroga.
🟠 Formula za obseg kroga
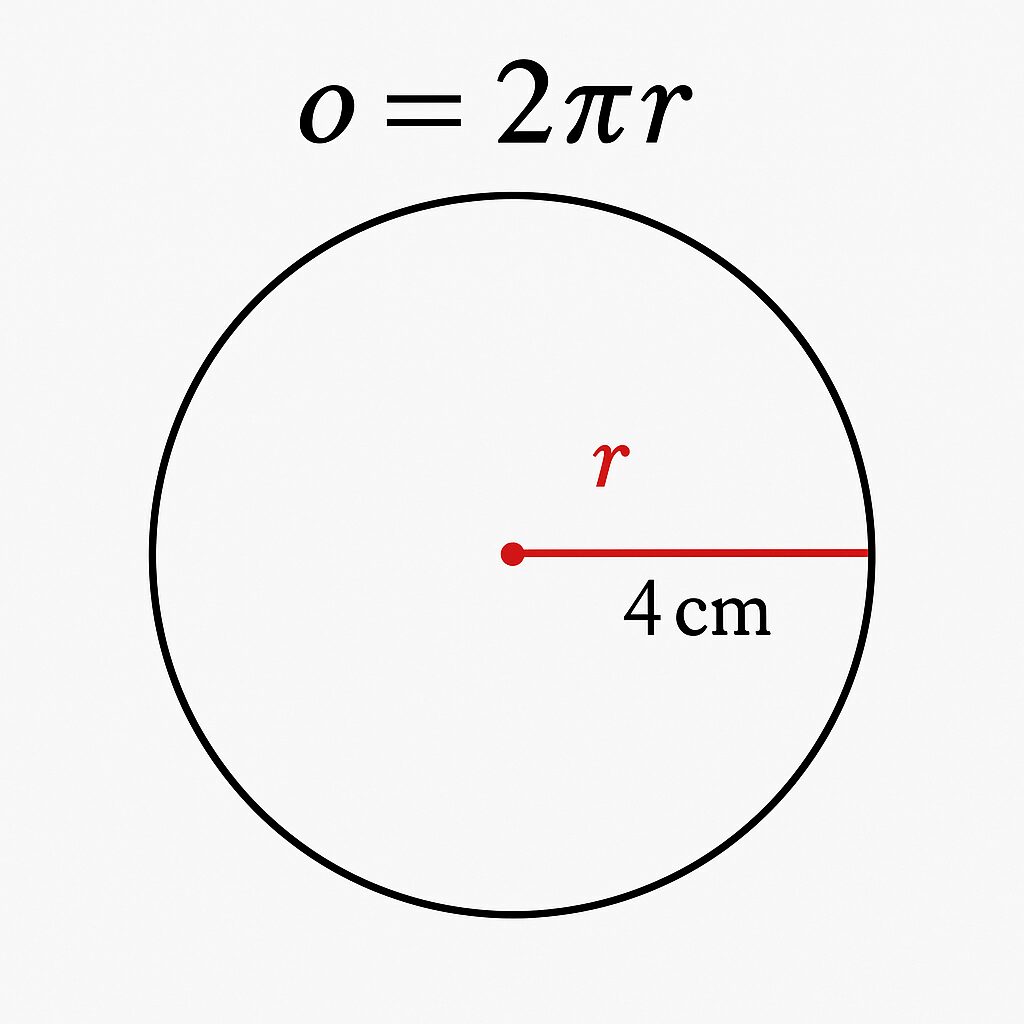
Obseg pove, kako dolg je rob kroga. Uporabimo formulo:
$o = 2\pi r$
Polmer ($r$) je razdalja od središča do točke na krožnici. Konstanta $\pi$ je približno enaka $3{,}14$.
Če je polmer $r = 4,\text{cm}$:
$o = 2 \cdot \pi \cdot 4$
$o = 8\pi \approx 25{,}12,\text{cm}$
🟠 Formula za ploščino kroga
Ploščina pokaže, koliko kvadratnih enot pokrije krog. Uporabimo formulo:
$p = \pi r^2$
To pomeni, da kvadriramo polmer in rezultat pomnožimo s $\pi$.
Če je polmer $r = 5,\text{cm}$:
$p = \pi \cdot 5^2$
$p = \pi \cdot 25$
$p \approx 78{,}5,\text{cm}^2$
Pri natančnem zapisu lahko pustimo rezultat v obliki izraza s $\pi$.
Obseg in ploščina trikotnika
Trikotnik ima tri stranice in tri kote. Glede na dane podatke lahko obseg in ploščino izračunamo na več načinov.
🟠 Obseg trikotnika
Seštejmo dolžine vseh treh stranic:
$o = a + b + c$
Če ima enakostranični trikotnik stranice dolžine $6,\text{cm}$:
$o = 6 + 6 + 6$
$o = 18,\text{cm}$
🟠 Ploščina trikotnika z višino
Če poznamo osnovnico $a$ in višino $v$ na to osnovnico, uporabimo:
$p = \frac{a \cdot v}{2}$
Višina je pravokotna razdalja od oglišča do osnovnice.
Če je $a = 10,\text{cm}$ in $v = 6,\text{cm}$:
$p = \frac{10 \cdot 6}{2}$
$p = \frac{60}{2}$
$p = 30,\text{cm}^2$
🟠 Heronova formula
Če poznamo vse tri stranice, najprej poiščimo polobseg:
$s = \frac{a + b + c}{2}$
Nato uporabimo formulo:
$p = \sqrt{s(s-a)(s-b)(s-c)}$
Če je $a = 5,\text{cm}$, $b = 6,\text{cm}$, $c = 7,\text{cm}$:
$s = \frac{5 + 6 + 7}{2} = \frac{18}{2} = 9$
$p = \sqrt{9(9- )(9-6)(9-7)}$
$p = \sqrt{9 \cdot 4 \cdot 3 \cdot 2}$
$p = \sqrt{216}$
$p \approx 14{,}7,\text{cm}^2`$
Obseg in ploščina pravokotnika
Pravokotnik ima dva para enako dolgih stranic. Vsi štirje koti so pravi, torej merijo $90^\circ$.
🟠 Formula za obseg pravokotnika
Obseg izračunamo tako, da seštejemo dolžine vseh stranic. Uporabimo formulo:
$o = 2a + 2b$
Če je dolžina $a = 8,\text{cm}$ in širina $b = 5,\text{cm}$:
$o = 2 \cdot 8 + 2 \cdot 5$
$o = 16 + 10$
$o = 26,\text{cm}$
🟠 Formula za ploščino pravokotnika
Ploščino dobimo z množenjem dolžine in širine:
$p = a \cdot b$
Če je $a = 8,\text{cm}$ in $b = 5,\text{cm}$:
$p = 8 \cdot 5$
$p = 40,\text{cm}^2$
Uspešno ste se prebili skozi snov in osvojili, kako se računa ploščina ter obseg osnovnih geometrijskih likov kvadrat, pravokotnik, krog in trikotnik. Želimo vam veliko uspeha pri reševanju matematičnih vaj. Povezave najdete spodaj 👇
Obseg in ploščina likov: vaje z rešitvami
1. Izračunaj obseg in ploščino kvadrata, če je diagonala dolga $d = 4{,}2\ \text{m}$.
2. Pravokotnik ABCD ima dolžino stranice $|AB| = a = 8{,}2\ \text{cm}$, diagonala pa meri $d = 2a$. Izračunaj ploščino pravokotnika.
3. Dolžini stranic pravokotnega vrta sta v razmerju $1 : 2$. Daljica, ki povezuje središči sosednjih stranic, je dolga $20\ \text{m}$. Izračunaj obseg in ploščino vrta.
4. Pravokotni vrt meri v dolžino $57\ \text{m}$ in v širino $42\ \text{m}$. Koliko kvadratnih metrov manjša bo ploščina vrta, če po notranjem robu zasadimo 60 cm široko okrasno ograjo?
5. Obseg paralelograma je $2{,}8\ \text{m}$. Ena stranica meri eno sedmino celotnega obsega. Izračunaj dolžini obeh stranic.
6. Eden notranji kot romba meri $120^\circ$, krajša diagonala pa je dolga $3{,}4\ \text{m}$. Izračunaj obseg romba.
7. Romb ABCD ima obseg $P = 112\ \text{dm}$, diagonala $BD$ pa je dolga $36\ \text{dm}$. Izračunaj dolžino diagonale $AC$.
8. V enakokrakem trapezu ABCD je $|AB| \parallel |CD|$, dolžina osnovnice $|CD| = c = 8\ \text{cm}$, višina $h = 7\ \text{cm}$, kot $∠CAB = 35^\circ$. Izračunaj ploščino trapeza.
9. Trapez ABCD ima osnovnici dolžin $a = 120\ \text{mm}$ in $c = 86\ \text{mm}$, ploščina pa znaša $A = 2,575\ \text{mm}^2$. Izračunaj višino trapeza.
10. Enakokraki trapez PQRS ima osnovnici $|PQ| = 120\ \text{mm}$ in $|RS| = 62\ \text{mm}$ ter krak $s = 48\ \text{mm}$. Izračunaj višino, dolžino diagonale in ploščino trapeza.
11. Zemljišče v obliki pravokotnega trapeza ima osnovnici dolžin $92\ \text{m}$ in $76\ \text{m}$, navpični krak pa je dolg $6{,}3\ \text{m}$. Izračunaj ploščino zemljišča in dolžino ograje.
12. Obseg enakokrakega trikotnika je $474\ \text{m}$. Osnova trikotnika je za $48\ \text{m}$ daljša od krakov. Izračunaj dolžine vseh stranic in ploščino trikotnika.
13. Pravokotni trikotnik ABC ima kateti $a = 5\ \text{cm}$ in $b = 8\ \text{cm}$. Trikotnik $A’B’C’$ je podoben trikotniku ABC in je $2{,}5$-krat manjši. Kolikšen delež ploščine trikotnika ABC zavzema ploščina trikotnika $A’B’C’$?
14. Pravokotni enakokraki trikotnik ima ploščino $32\ \text{cm}^2$. Kolikšen je njegov obseg?
15. Enakostranični trikotnik ima obseg $36\ \text{dm}$. Kolikšna je njegova ploščina?
16. Trikotnik ABC ima stranice dolžin $a = 14\ \text{cm}$, $b = 20\ \text{cm}$ in $c = 7{,}5\ \text{cm}$. Izračunaj velikosti notranjih kotov in ploščino trikotnika.
17. Trikotnik ABC ima podano stranico $a = 8{,}4$, kot $\beta = 105^\circ 35’$ in težnico na stranico $a$, $m_a = 12{,}5$. Izračunaj obseg, ploščino in preostala kota.
18. Trikotnik ABC ima podano ploščino $A = 501{,}9$, kot $\alpha = 15^\circ 28’$ in kot $\beta = 45^\circ$. Izračunaj vse stranice in notranje kote trikotnika.
19. Paralelogram ABCD ima ploščino $40\ \text{cm}^2$, $|AB| = 8{,}5\ \text{cm}$ in $|BC| = 5{,}65\ \text{cm}$. Izračunaj dolžini diagonal.
20. Izračunaj ploščino pravilnega šestkotnika, če je polmer včrtane krožnice $\rho = 4\ \text{cm}$.
21. V pravilnem šestkotniku ABCDEF je diagonala $|AC| = 12\ \text{cm}$. Izračunaj dolžino stranice in ploščino šestkotnika.
22. Izračunaj obseg kroga, če je njegova ploščina $706{,}5\ \text{cm}^2$.
23. Izračunaj ploščino kroga, če je njegov obseg $94{,}2\ \text{dm}$.
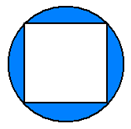
24. Kvadrat na sliki ima stranico dolgo $8\ \text{cm}$. Izračunaj ploščino obarvanega dela kroga.
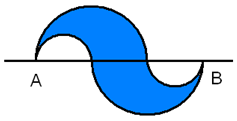
25. Na sliki sta dva večja in dva manjša polkroga. Polmer večjega je dvakrat večji od polmera manjšega. Če je $|AB| = 12\ \text{cm}$, izračunaj ploščino obarvanega vzorca.
Geometrija v ravnini: vaje z rešitvami
Če iščete učitelja, ki vam lahko pomaga osvojiti, kako se izračuna ploščina kroga in ploščina kvadrata, hitro poiščite “inštruktor matematike Maribor” ali “inštrukcije matematike Velenje”. Na meet’n’learn ali v facebook skupini se lahko v trenutku povežete z najboljšim zasebnim učiteljem.
