Uvod v kompleksna števila
Kompleksna števila so razširitev realnih števil in omogočajo reševanje matematičnih problemov, ki jih z realnimi števili ni mogoče rešiti.
Osnova za kompleksna števila je imaginarna enota, označena z 𝑖, za katero velja, da je 𝑖2=−1.
Ta lastnost imaginarnega števila nam omogoča, da definiramo kompleksna števila na način, ki zajema tako realne kot imaginarne komponente.
Kaj je kompleksno število
Kompleksno število je število, ki se lahko izrazi v obliki 𝑎+𝑏𝑖, kjer sta 𝑎 in 𝑏 realni števili, 𝑖 pa je imaginarno število. V tem izrazu 𝑎 predstavlja realni del, 𝑏 pa imaginarni del kompleksnega števila.
Kompleksna števila primer
- 2+3𝑖
- −1+2𝑖
- 0+𝑖
Kompleksna števila lahko predstavimo v kompleksni ravnini, kjer realni del 𝑎 predstavimo na horizontalni osi, imaginarni del 𝑏 pa na vertikalni osi. Vsako kompleksno število je v tej ravnini predstavljeno kot točka ali vektor.
Matematične operacije s kompleksnimi števili
Seštevanje kompleksnih števil
Za seštevanje dveh kompleksnih števil (𝑎+𝑏𝑖) in (𝑐+𝑑𝑖) preprosto seštejemo njihove realne dele in njihove imaginarne dele posebej.
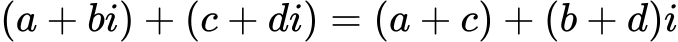
Odštevanje kompleksnih števil
Odštevanje poteka podobno, le realne dele in imaginarne dele odštejemo.
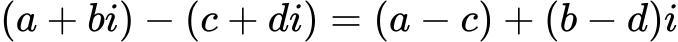
Množenje kompleksnih števil
Množenje kompleksnih števil zahteva uporabo distributivnostnega zakona, pri čemer upoštevamo, da je 𝑖2=−1.
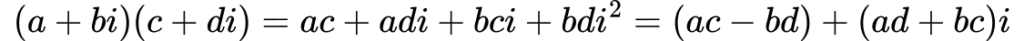
Deljenje kompleksnih števil
Deljenje kompleksnih števil izvedemo tako, da števec in imenovalec pomnožimo s konjugirano vrednostjo imenovalca.

Absolutna vrednost kompleksnega števila
Absolutna vrednost kompleksnega števila 𝑧=𝑎+𝑏𝑖 je definirana kot razdalja od izhodišča do točke v kompleksni ravnini, ki jo določa število 𝑧. Absolutna vrednost kompleksnega števila se izračuna po formuli:
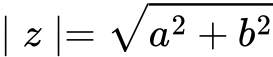
Absolutna vrednost kompleksnega števila predstavlja osnovno znanje o kompleksnih številih, ki služi kot temelj za nadaljnje študije in uporabe v matematiki.
Eulerjeva formula in njena uporaba
Eulerjeva formula je ena izmed najbolj osupljivih povezav v matematiki, ki povezuje eksponentno funkcijo z osnovnim številom 𝑒 s trigonometričnimi funkcijami in imaginarno enoto 𝑖. Eulerjeva formula je nepogrešljiva v različnih tehničnih in znanstvenih disciplinah, vključno z elektrotehniko in kvantno mehaniko.
Eulerjeva formula je izpeljana iz Taylorjeve vrste za eksponentno, sinusno in kosinusno funkcijo. Če zamenjamo 𝑥 z 𝑖𝑥 v Taylorjevi vrsti za 𝑒𝑥, dobimo:
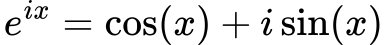
Zakaj je Eulerjeva formula tako pomembna
Eulerjeva formula je temelj za analizo periodičnih pojavov in valovanj v fiziki in inženirstvu. Omogoča preoblikovanje kompleksnih eksponentnih izrazov v bolj obvladljive trigonometrične oblike, kar je ključno za analizo signalov in sistemov.
Kompleksna števila vaje z rešitvami
Spodaj smo pripravili matematične naloge, da boste lahko vadili kompleksna števila in kaj je absolutna vrednost kompleksnega števila. Rešite jih in utrdite znanje kompleksnih števil, absolutne vrednosti in Eulerjevo formulo. Rešitve najdete čisto spodaj. ⬇️
1. Poenostavite izraz s kompleksnimi števili:
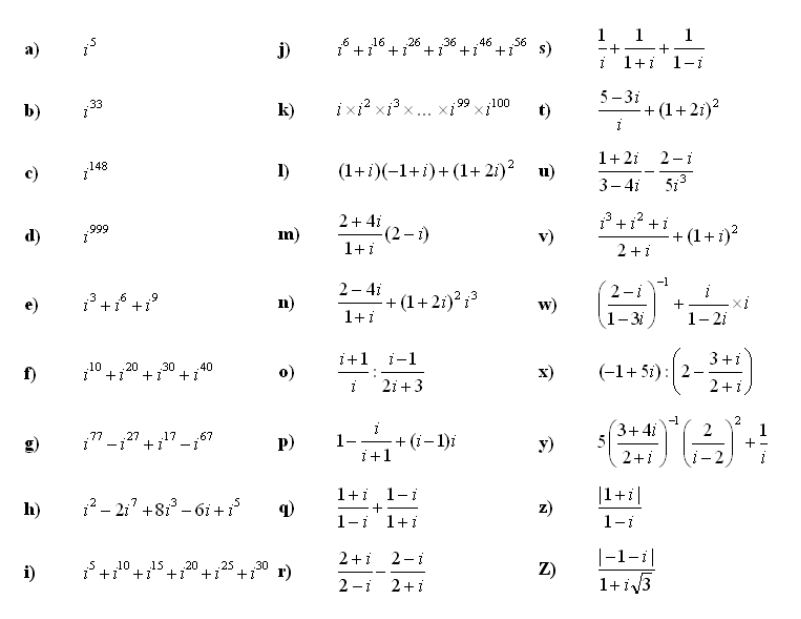
2. Poiščite absolutno vrednost kompleksnega števila:

3. Poiščite vsoto, razliko in produkt kompleksnih števil x in y:
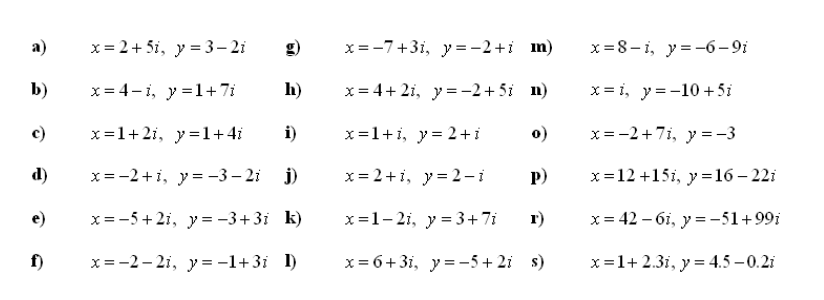
4. Poiščite količnik kompleksnih števil:
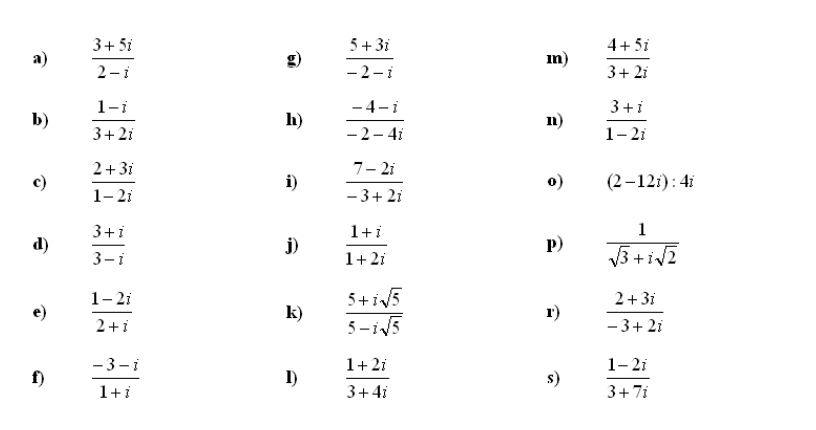
5. Dano kompleksno število zapišite v trigonometrični obliki:

6. Dano kompleksno število zapišite v algebrski obliki:

7. Poiščite moč kompleksnega števila:
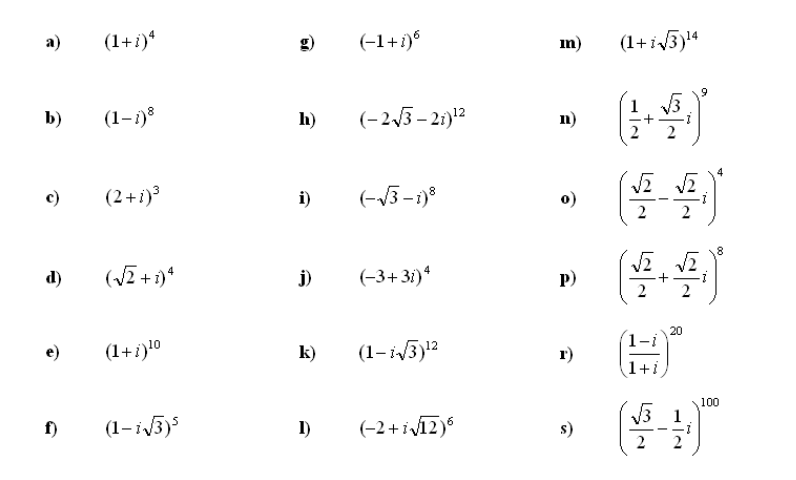
8. Rešite enačbe s kompleksnimi števili:
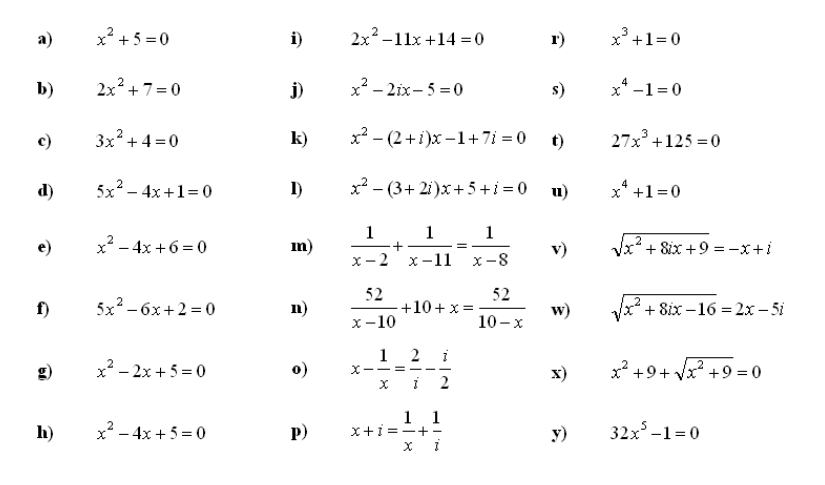
Dodatne vaje za množice in števila
Iščete učitelja, ki vam lahko pomaga osvojiti, kaj so kompleksna števila in Eulerjeva formula ter kako se določi absolutna vrednost kompleksnega števila? Hitro poiščite “inštruktor matematike Celje” ali “inštrukcije matematike Maribor”. Na platformah, kot je meet’n’learn, se lahko v trenutku povežete z najboljšim zasebnim učiteljem.