Trikotnik – osnovne značilnosti in vrste
Trikotnik ima tri oglišča, tri stranice in tri notranje kote. Oglišča označimo z $A$, $B$ in $C$, stranice s $a$, $b$ in $c$, kote pa z $\alpha$, $\beta$ in $\gamma$. Točke $A$, $B$ in $C$ ne smejo ležati na isti premici. Vedno velja:
$\alpha + \beta + \gamma = 180^\circ$
Trikotnike razvrstimo glede na dolžine stranic ali velikosti notranjih kotov.
🟠 Vrste trikotnikov glede na dolžine stranic
Enakostranični trikotnik
Vse tri stranice so enako dolge: $a = b = c$. Tudi vsi trije koti so enaki in merijo $60^\circ$.
Enakokraki trikotnik
Dve stranici sta enaki. Imenujemo ju kraka. Tretja stranica je osnovnica. Kota ob osnovnici sta enaka.
Raznostranični trikotnik
Vse stranice so različno dolge. Vsak kot ima različno velikost.
🟠 Vrste trikotnikov glede na notranje kote
Ostrokotni trikotnik
Vsi notranji koti so ostri, torej manjši od $90^\circ$.
Pravokotni trikotnik
Eden od notranjih kotov meri $90^\circ$. Nasproti tega kota leži hipotenuza, druga dva kota sta ostra, preostali stranici pa sta kateti.
Topokotni trikotnik
Eden od kotov meri več kot $90^\circ$. Druga dva kota sta manjša od $90^\circ$.
V nobenem trikotniku ne moreta biti hkrati dva kota topa ali dva kota prava, saj bi bila vsota večja od $180^\circ$.
Lastnosti in elementi trikotnika
Trikotnik ima tri stranice, tri notranje kote, tri višine, tri težiščnice in tri simetrale. Z njimi računamo ploščino, obseg ali druge značilnosti trikotnika.
🟠 Notranji in zunanji koti
Vsota notranjih kotov v trikotniku je vedno $180^\circ$:
$\alpha + \beta + \gamma = 180^\circ$
Zunanji kot je sokot notranjemu in ga dobimo, če eno stranico podaljšamo. Vsak zunanji kot je enak vsoti preostalih dveh notranjih kotov: $\alpha’ = \beta + \gamma$
Skupna vsota zunanjih kotov trikotnika je $360^\circ$:
$\alpha’ + \beta’ + \gamma’ = 360^\circ$
🟠 Višina trikotnika in višinska točka
Višino narišemo iz oglišča pravokotno na nosilko nasprotne stranice. Trikotnik ima tri višine.
Poiščimo presečišče vseh treh višin. Ta točka se imenuje višinska točka. V ostrokotnem trikotniku leži znotraj lika, v pravokotnem v oglišču pravega kota, v topokotnem pa zunaj trikotnika.
🟠 Težišče in težiščnice
Težiščnica poteka od oglišča do razpolovišča nasprotne stranice. Vsak trikotnik ima tri težiščnice.
Vse tri težiščnice se sekajo v eni točki. Točko označimo s $T$ in jo imenujemo težišče. Težišče vedno leži znotraj trikotnika. Deli vsako težiščnico v razmerju $2 : 1$, kjer je daljši del bližje oglišču.
Obseg trikotnika – formula in primeri
Obseg trikotnika dobimo tako, da seštejemo dolžine vseh treh stranic. Oznake naj bodo $a$, $b$ in $c$. Pri posebnih trikotnikih lahko formulo poenostavimo.
🟠 Obseg za splošni trikotnik
Za vsak trikotnik uporabimo formulo:
$o = a + b + c$
Primer:
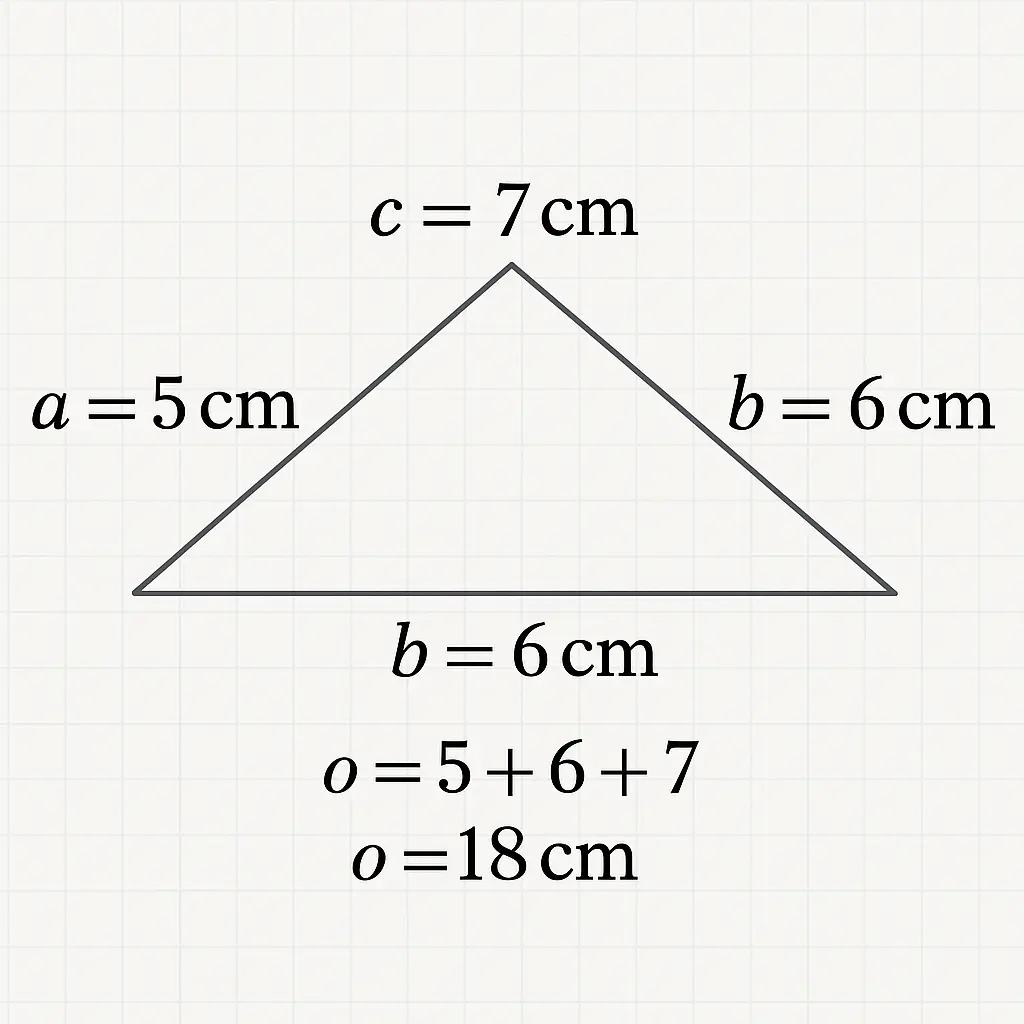
Naj bo $a = 5,\text{cm}$, $b = 6,\text{cm}$ in $c = 7,\text{cm}$.
Izračunajmo obseg:
$o = 5 + 6 + 7$
$o = 18,\text{cm}$
Obseg enakokrakega in enakostraničnega trikotnika
V enakostraničnem trikotniku so vse tri stranice dolge enako. Če označimo dolžino stranice z $a$, potem je obseg:
$o = 3a$
🟠 Primer:
Če je $a = 4,\text{cm}$, dobimo:
$o = 3 \cdot 4 = 12,\text{cm}$
V enakokrakem trikotniku imata dve stranici dolžino $a$, tretja (osnovnica) pa dolžino $b$. Uporabimo formulo:
$o = 2a + b$
🟠 Primer:
Če je $a = 5,\text{cm}$ in $b = 6,\text{cm}$, potem je:
$o = 2 \cdot 5 + 6 = 10 + 6 = 16,\text{cm}$
Ploščina trikotnika – vse formule in posebni primeri
Ploščina trikotnika pove, kolikšen del ravnine lik omejuje. Izračunamo jo na več načinov, odvisno od znanih podatkov.
🟠 Osnovna formula za ploščino trikotnika
Če poznamo dolžino stranice $c$ in višino $v_c$ na to stranico, uporabimo formulo:
$p = \frac{c \cdot v_c}{2}$
Primer:
Naj bo $c = 8$ in $v_c = 5$. Izračunamo ploščino:
$p = \frac{8 \cdot 5}{2}$
$p = \frac{40}{2}$
$p = 20$
🟠 Ploščina pravokotnega trikotnika
V pravokotnem trikotniku uporabimo kateti $a$ in $b$:
$p = \frac{a \cdot b}{2}$
Primer:
Če je $a = 6$ in $b = 4$, potem:
$p = \frac{6 \cdot 4}{2}$
$p = \frac{24}{2}$
$p = 12$
🟠 Heronova formula za ploščino
Ko poznamo vse tri stranice $a$, $b$ in $c$, uporabimo Heronovo formulo. Najprej izračunamo polobseg:
$s = \frac{a + b + c}{2}$
Nato izračunamo ploščino:
$p = \sqrt{s(s-a)(s-b)(s-c)}$
Primer:
Naj bo $a = 7$, $b = 8$ in $c = 9$.
Najprej polobseg:
$s = \frac{7 + 8 + 9}{2}$
$s = \frac{24}{2}$
$s = 12$
Vstavimo v formulo:
$p = \sqrt{12(12-7)(12-8)(12-9)}$
$p = \sqrt{12 \cdot 5 \cdot 4 \cdot 3}$
$p = \sqrt{720}$
$p \approx 26.83$
Pitagorov izrek in ploščina pravokotnega trikotnika
Pitagorov izrek velja samo za pravokotni trikotnik. Uporabimo ga, kadar poznamo dolžini dveh stranic in iščemo tretjo. Prav tako z njim preverimo, ali ima trikotnik pravi kot.
🟠 Pitagorov izrek – osnovna oblika
Če je $c$ hipotenuza, $a$ in $b$ pa kateti, uporabimo formulo:
$c^2 = a^2 + b^2$
Primer:
Naj bo $a = 6,\text{cm}$ in $b = 8,\text{cm}$. Poiščimo $c$:
$c^2 = 6^2 + 8^2$
$c^2 = 36 + 64$
$c^2 = 100$
$c = \sqrt{100}$
$c = 10,\text{cm}$
🟠 Ploščina pravokotnega trikotnika
Ploščino pravokotnega trikotnika izračunamo tako:
$p = \frac{a \cdot b}{2}$
$a$ in $b$ sta kateti, ki tvorita pravi kot.
Primer:
Naj bo $a = 7,\text{cm}$ in $b = 4,\text{cm}$:
$p = \frac{7 \cdot 4}{2}$
$p = \frac{28}{2}$
$p = 14,\text{cm}^2$
🟠 Pitagorejske trojice
Pitagorejske trojice so skupine naravnih števil, ki ustrezajo Pitagorovemu izreku.
Primer trojice:
$3, 4, 5$ → $3^2 + 4^2 = 9 + 16 = 25 = 5^2$
Osnovne pitagorejske trojice:
| Kateta $a$ | Kateta $b$ | Hipotenuza $c$ |
|---|---|---|
| $3$ | $4$ | $5$ |
| $5$ | $12$ | $13$ |
| $7$ | $24$ | $25$ |
| $8$ | $15$ | $17$ |
| $9$ | $40$ | $41$ |
| $11$ | $60$ | $61$ |
Če vsako število v trojici pomnožimo z istim faktorjem, dobimo novo pitagorejsko trojico.
Primer: $3, 4, 5$ → pomnožimo s $2$: $6, 8, 10$
Razreševanje trikotnika – izračun kotov in stranic
Če poznamo nekaj stranic in/ali kotov v splošnem trikotniku, lahko manjkajoče podatke izračunamo s pomočjo sinusnega in kosinusnega izreka.
🟠 Sinusni izrek
Sinusni izrek povezuje dolžine stranic in njihove nasprotne kote. Velja za vse trikotnike, ne glede na vrste kotov ali dolžine stranic.
Formula:
$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma}$
Z njim lahko poiščemo manjkajoči kot ali stranico, če poznamo vsaj eno stranico in njen nasprotni kot.
Primer:
Naj bo $a = 6$, $\alpha = 40^\circ$, $\beta = 60^\circ$. Poiščimo $b$:
$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta}$
$\frac{6}{\sin 40^\circ} = \frac{b}{\sin 60^\circ}$
$b = \frac{6 \cdot \sin 60^\circ}{\sin 40^\circ}$
Vstavimo vrednosti (uporabimo kalkulator za sinusne vrednosti):
$b \approx \frac{6 \cdot 0.866}{0.6428} \approx \frac{5.196}{0.6428} \approx 8.08$
🟠 Kosinusni izrek
Kosinusni izrek uporabimo, kadar poznamo dve stranici in vmesni kot ali vse tri stranice.
Formula:
$a^2 = b^2 + c^2-2bc \cos \alpha$
Lahko ga preuredimo tudi za izračun kota:
$\cos \alpha = \frac{b^2 + c^2-a^2}{2bc}$
Primer:
Naj bo $b = 7$, $c = 5$, $\alpha = 60^\circ$. Poiščimo $a$:
$a^2 = 7^2 + 5^2-2 \cdot 7 \cdot 5 \cdot \cos 60^\circ$
$a^2 = 49 + 25-70 \cdot 0.5$
$a^2 = 74-35$
$a^2 = 39$
$a = \sqrt{39} \approx 6.24$
Uspešno ste se prebili skozi snov in osvojili, kako se računa ploščina trikotnika in kaj je Pitagorov izrek.
Želimo vam veliko uspeha pri reševanju matematičnih vaj. Povezave najdete spodaj 👇
Trikotnik in Pitagorov izrek: vaje z rešitvami
1. Enakostranični trikotnik ima stranico dolgo $4\ \text{cm}$. Izračunaj njegov obseg, ploščino ter velikost notranjih in zunanjih kotov.
2. Zunanji kot enakokrakega trikotnika meri $87^\circ$. Določi notranje kote trikotnika.
3. Kateta pravokotnega trikotnika meri $12\ \text{cm}$. Koliko je oddaljeno središče hipotenuze od druge katete?
4. Trikotnik ABC ima kota $\alpha = 30^\circ$ in $\beta = 45^\circ$. Kolikšen je kot med višinama iz stranic $BC$ in $AB$?
5. Pravokotni trikotnik ima hipotenuzo dolgo $50\ \text{cm}$. Obseg je $P = 1{,}2\ \text{m}$, ploščina pa $A = 6\ \text{dm}^2$. Izračunaj dolžini katet in vse notranje kote.
6. Enakokraki trikotnik ABC ima osnovnico $|AB| = 12\ \text{cm}$, višina iz kota $C$ pa meri $10\ \text{cm}$. Izračunaj dolžino kraka in težnico na krak.
7. Lestev dolžine $8{,}5\ \text{m}$ naslanja na navpični zid. Spodnji konec je oddaljen $1{,}8\ \text{m}$ od zidu.
a) Do katere višine sega vrh lestve?
b) Pod kakšnim kotom je lestev naslonjena na zid?
8. V trikotniku MPN velja $|NP| = 7\ \text{cm}$, $|PM| = 13\ \text{cm}$ in višina na stranico $MN$ je dolga $|PP’| = 5\ \text{cm}$. Izračunaj dolžino stranice $MN$.
9. Obseg enakokrakega trikotnika ABC znaša $60\ \text{cm}$, kvadrat višine iz osnovnice pa je $h_c^2 = 60$. Izračunaj dolžino osnovnice in krakov.
10. V enakokrakem trikotniku ABC meri kot pri oglišču $A$ natančno $42^\circ$. Na kraku $AB$ je točka $D$, kjer velja $|CB| = |CD|$. Določi kot $\angle ACD$.
11. V trikotniku ABC velja $|\alpha| = 2|\beta|$ in $|\beta| = 3|\gamma|$. Izračunaj vse kote trikotnika.
12. Trije krogi z radiji $r_1 = 5\ \text{cm}$, $r_2 = 10\ \text{cm}$ in $r_3 = 12\ \text{cm}$ se dotikajo od zunaj. Določi dolžine stranic in velikosti kotov trikotnika, ki ga določajo središča krogov.
13. V trikotniku velja razmerje kotov $\alpha : \beta : \gamma = 3 : 4 : 5$, nasproti kota $\alpha$ pa leži stranica dolžine $a = \sqrt{2}$. Izračunaj vse kote in dolžine stranic.
14. Na vrhu hriba stoji stolp visok $30\ \text{m}$. Z določene točke v dolini vidimo njegov vrh in vznožje pod kotoma višine $\alpha = 28^\circ30’$ in $\beta = 30^\circ40’$. Koliko metrov nad vodoravno lego opazovanja je vrh hriba?
15. Z 20 m visokega stolpa, ki stoji 20 m od reke, opazimo širino reke pod kotom $15^\circ$. Koliko je široka reka?
16. Trikotnik ABC ima podane vrednosti: $\alpha = 51^\circ19’$, $\beta = 67^\circ38’$ in višino na stranico $c$, $h_c = 28$. Izračunaj stranice in preostali kot.
17. V trikotniku ABC je kot $\alpha$ nasproti stranice $a = \sqrt{3}$ dvakrat večji od kota $\beta$, nasproti stranice $b = 1$. Izračunaj obseg in ploščino trikotnika.
18. Trikotnik ABC ima kota $\alpha = 113^\circ$, $\beta = 48^\circ$, polmer opisane krožnice pa je $r = 10\ \text{cm}$. Izračunaj dolžine vseh stranic.
19. V trikotniku ABC so podani: $a = 8{,}4$, $\beta = 105^\circ35’$, težnica na stranico $a$, $m_a = 12{,}5$. Izračunaj dolžine preostalih stranic in velikosti kotov.
20. Trije krogi z radiji $r_1 = 5$, $r_2 = 4$ in $r_3 = 6$ se dotikajo od zunaj. Izračunaj ploščino lika, ki leži med krogi.
21. Preveri, ali ima trikotnik s stranicami $a = 11$, $b = 14$, $c = 18$ topi kot.
22. Trikotnik ABC ima ploščino $A = 501{,}9$, $\alpha = 15^\circ28’$, $\beta = 45^\circ$. Izračunaj dolžine stranic in preostali kot.
23. Dve sili velikosti $72\ \text{N}$ in $58\ \text{N}$ delujeta v skupni točki pod kotom $72^\circ30’$. Izračunaj velikost rezultante.
24. Paralelogram ABCD ima ploščino $40\ \text{cm}^2$, $|AB| = 8{,}5\ \text{cm}$ in $|BC| = 5{,}65\ \text{cm}$. Izračunaj dolžini diagonal.
25. V pravokotnem trikotniku ABC poznamo težnici $m_a = 12$ in $m_b = 15$. Izračunaj dolžine vseh stranic.
26. Preveri, ali je trikotnik s stranicami dolžin $2$, $n-n-1$, $n + n-1$ pravokoten.
27. Krog ima včrtan in opisan kvadrat. Razlika ploščin teh dveh kvadratov je $18$. Izračunaj radij kroga.
28. V krogu je tetiva, ki je od središča oddaljena $8\ \text{cm}$, dolga za $13\ \text{cm}$ več kot je radij kroga. Izračunaj radij kroga.
29. Romb ima ploščino $A = 120$, razmerje diagonal pa je $e : f = 5 : 12$. Izračunaj dolžino stranice $a$, višine $h$ ter diagonali $e$ in $f$.
30. Pravokotni trikotnik ABC ima stranico $a = 5$ in višino na hipotenuzo $h_c = 3$. Izračunaj dolžini stranic $b$ in $c$.
Geometrija v ravnini: vaje z rešitvami
Če iščete učitelja, ki vam lahko pomaga osvojiti, kako se izračuna ploščina trikotnika in kaj je Pitagorov izrek, hitro poiščite “inštruktor matematike Maribor” ali “inštrukcije matematike Velenje”. Na meet’n’learn ali v Facebook skupini se lahko v trenutku povežete z najboljšim zasebnim učiteljem.
