Kotne funkcije v pravokotnem trikotniku
🟠 Definicija kotne funkcije glede na stranice
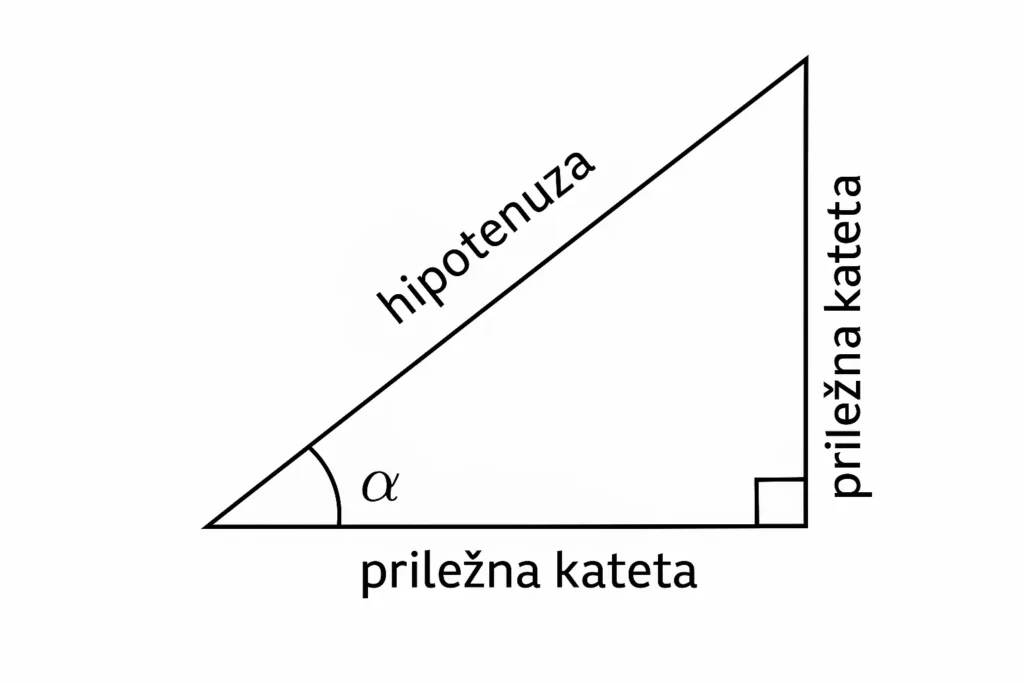
V pravokotnem trikotniku imenujemo stranici ob pravem kotu kateti, najdaljšo stranico pa hipotenuza. Glede na razmerja med stranicami definiramo osnovne kotne funkcije:
$\sin \alpha = \frac{\text{nasprotna kateta}}{\text{hipotenuza}}$
$\cos \alpha = \frac{\text{priležna kateta}}{\text{hipotenuza}}$
$\tan \alpha = \frac{\text{nasprotna kateta}}{\text{priležna kateta}}$
$\cot \alpha = \frac{\text{priležna kateta}}{\text{nasprotna kateta}}$
Za kot $\alpha$ vedno vzamemo enega izmed ostrih kotov.
🟠 Vrednosti kotnih funkcij v enotski krožnici
Za kote $30^\circ$, $45^\circ$ in $60^\circ$ pogosto uporabljamo točne vrednosti. Te si zapomnimo, ker jih pogosto srečamo pri računih.
$\sin 30^\circ = \frac{1}{2}$, $\cos 30^\circ = \frac{\sqrt{3}}{2}$, $\tan 30^\circ = \frac{1}{\sqrt{3}}$
$\sin 45^\circ = \frac{\sqrt{2}}{2}$, $\cos 45^\circ = \frac{\sqrt{2}}{2}$, $\tan 45^\circ = 1$
$\sin 60^\circ = \frac{\sqrt{3}}{2}$, $\cos 60^\circ = \frac{1}{2}$, $\tan 60^\circ = \sqrt{3}$
Te vrednosti je dobro poznati tudi brez kalkulatorja.
🟠 Tabela osnovnih vrednosti in predznaki v kvadrantih
Kotne funkcije imajo v posameznih kvadrantih različne predznake:
| Kvadrant | $\sin$ | $\cos$ | $\tan$ |
|---|---|---|---|
| I | + | + | + |
| II | + | − | − |
| III | − | − | + |
| IV | − | + | − |
Uporabimo pravilo: “V prvi vse, v drugi samo sinus, v tretji tangens, v četrti kosinus.”
Pitagorov izrek in pravokotni trikotnik
🟠 Pitagorov izrek – osnovna oblika
V pravokotnem trikotniku je hipotenuza najdaljša stranica in leži nasproti pravega kota. Velja enačba:
$c^2 = a^2 + b^2$
Stranici $a$ in $b$ sta kateti, $c$ je hipotenuza. Enačba velja, če je kot med stranicama $a$ in $b$ prav.
🟠 Pitagorejske trojice in tipični primeri
Pitagorejska trojica je skupina treh naravnih števil, ki ustrezajo enačbi $c^2 = a^2 + b^2$.
Najbolj znana je:
$3^2 + 4^2 = 9 + 16 = 25 = 5^2$
Torej: $a = 3$, $b = 4$, $c = 5$
Druge znane trojice so $5, 12, 13$ in $8, 15, 17$.
🟠 Uporaba Pitagorovega izreka pri iskanju stranic
Če poznamo dolžini dveh stranic, izračunamo tretjo.
Če je $a = 6$ in $b = 8$, potem:
$c^2 = 6^2 + 8^2$
$c^2 = 36 + 64$
$c^2 = 100$
$c = \sqrt{100}$
$c = 10$
Poiščimo še drugo stranico. Če je $c = 13$ in $a = 5$, potem:
$b^2 = 13^2-5^2$
$b^2 = 169-25$
$b^2 = 144$
$b = \sqrt{144}$
$b = 12$
Ploščina trikotnika v povezavi s kotnimi funkcijami
🟠 Formula za pravokotni trikotnik
Če imamo pravokotni trikotnik, lahko ploščino izračunamo tako, da vzamemo produkt katet in ga delimo z $2$:
$p = \frac{a \cdot b}{2}$
$a$ in $b$ sta kateti, torej stranici, ki oklepata pravi kot.
🟠 Ploščina trikotnika z znanim kotom med stranicama
Če imamo splošen trikotnik in poznamo dolžini dveh stranic ter kot med njima, uporabimo formulo:
$p = \frac{1}{2}ab\sin \gamma$
$a$ in $b$ sta stranici, $\gamma$ je kot med njima.
Kot mora biti izražen v stopinjah ali radianih, glede na nastavitve kalkulatorja.
Sinusni izrek za poljubni trikotnik
🟠 Formula sinusnega izreka
V poljubnem trikotniku povežemo dolžine stranic in nasprotne kote z izrazom:
$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma}$
$a$, $b$ in $c$ so dolžine stranic, $\alpha$, $\beta$ in $\gamma$ pa pripadajoči nasprotni koti.
🟠Kdaj uporabimo sinusni izrek
Sinusni izrek uporabimo, kadar poznamo en par stranica–nasprotni kot in še eno dodatno informacijo, na primer drugo stranico ali drugi kot. Primeren je za primere ASA, AAS ali SSA. Z njim izračunamo manjkajočo stranico ali kot.
🟠 Rešen primer s podatki in izračunom
Podano: $a = 7$, $\alpha = 40^\circ$, $\beta = 60^\circ$. Poiščimo $b$.
Uporabimo sinusni izrek:
$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta}$
$\frac{7}{\sin 40^\circ} = \frac{b}{\sin 60^\circ}$
$\frac{7}{0.6428} = \frac{b}{0.8660}$
$10.9 = \frac{b}{0.8660}$
$b = 10.9 \cdot 0.8660$
$b \approx 9.4$
Kosinusni izrek in razreševanje trikotnika
🟠 Formula kosinusnega izreka za stranico
Če poznamo dve stranici trikotnika in kot med njima, uporabimo kosinusni izrek:
$a^2 = b^2 + c^2-2bc\cos \alpha$
$a$ je stranica nasproti kota $\alpha$, $b$ in $c$ sta sosednji stranici.
🟠 Izračun kota s kosinusnim izrekom
Če poznamo vse tri stranice, lahko preuredimo enačbo in izračunamo kot:
$\cos \alpha = \frac{b^2 + c^2-a^2}{2bc}$
S tem izrazom izračunamo $\cos \alpha$, nato poiščemo kot s funkcijo $\cos^{-1}$.
🟠 Primer, kjer poznamo vse tri stranice
Podano: $a = 7$, $b = 8$, $c = 10$. Poiščimo kot $\alpha$:
$\cos \alpha = \frac{8^2 + 10^2-7^2}{2 \cdot 8 \cdot 10}$
$\cos \alpha = \frac{64 + 100-49}{160}$
$\cos \alpha = \frac{115}{160}$
$\cos \alpha = 0.71875$
$\alpha = \cos^{-1}(0.71875)$
$\alpha \approx 44^\circ$
Primerjava: sinusni izrek ali kosinusni izrek?
Če poznamo en kot in nasproti ležečo stranico, uporabimo sinusni izrek.
Če poznamo dve stranici in kot med njima ali vse tri stranice, uporabimo kosinusni izrek.
Povzetek:
$a$, $\alpha$, $b$ → sinusni izrek za kot ali stranico
$\alpha$, $a$, $b$ → sinusni izrek
$a$, $b$, $\gamma$ → kosinusni izrek
$a$, $b$, $c$ → kosinusni izrek za kot
Uspešno ste se prebili skozi snov in osvojili, kaj sta sinusni in kosinusni izrek. Želimo vam veliko uspeha pri reševanju matematičnih vaj. Povezave najdete spodaj 👇
Trigonometrija in kotne funkcije: vaje z rešitvami
1. V pravokotnem trikotniku ABC izračunajte preostale stranice in kote. Uporabite Pitagorov izrek ter kotne funkcije sinus, kosinus, tangens in kotangens:
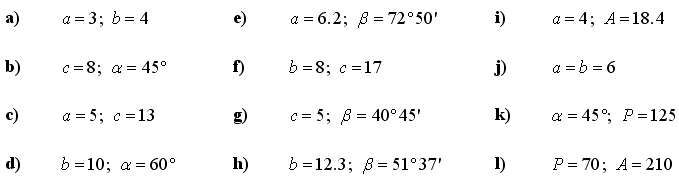
2. V trikotniku ABC izračunajte preostale stranice in kote. Uporabite sinusni izrek in kosinusni izrek:
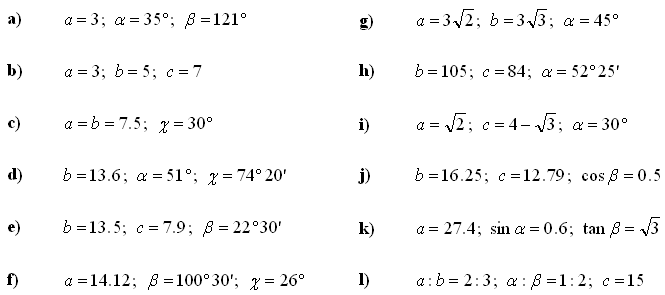
3. Določite vse kotne funkcije, če poznamo vrednost ene izmed njih:
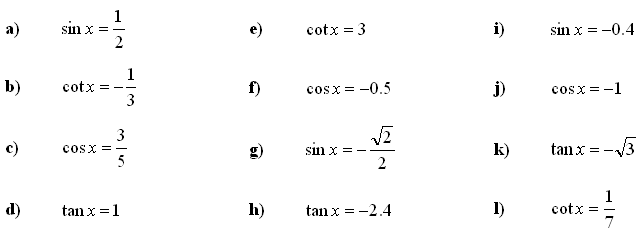
4. Poenostavite podane trigonometrične izraze:

Geometrija v ravnini: vaje z rešitvami
Če iščete učitelja, ki vam lahko pomaga osvojiti kotne funkcije ter sinusni in kosinusni izrek, hitro poiščite “inštruktor matematike Maribor” ali “inštrukcije matematike Velenje”. Na meet’n’learn ali v facebook skupini se lahko v trenutku povežete z najboljšim zasebnim učiteljem.
